Hace unos días publiqué una entrada en la que estudiábamos las matemáticas que podemos encontrar en la bandera de Cabra. Allí os dije que dedicaríamos otra a la marca turística de Cabra, así que aquí está.
Según la Resolución de 13 de junio de 2014, el símbolo pretende recoger los aspectos más significativos de Cabra como destino histórico. Como fondo aparece la estrella andalusí de ocho puntas y una media luna embute la imagen estilizada de una cabra, que evidentemente, hace referencia al nombre de nuestra ciudad. Además, con el fin de situarla geográficamente se incluye el eslogan “CABRA, la cordobesa”, cuyas fuentes están en proporción 2:1 (el nombre de Cabra tiene el doble de puntos que el lema “la cordobesa”) (Eso es lo que pone en la resolución, pero a mí no me parece que se cumpla y veo “CABRA” escrito mucho más grande que el doble de “la cordobesa”. Tipógrafos, arrojen luz sobre esta cuestión).

La estrella andalusí de ocho puntas se construye a partir de dos cuadrados iguales concéntricos, uno de ellos girando 45o sobre el otro, como se ve en la imagen:
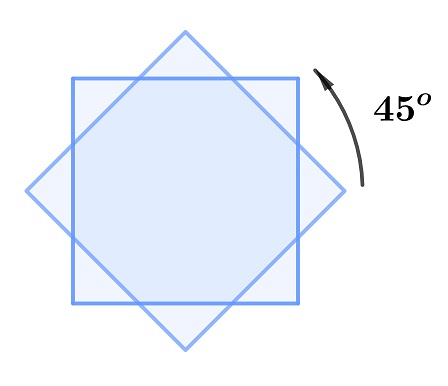
Si nos fijamos, dentro de esta estrella hay una circunferencia de la que no se dice nada en la Resolución, a pesar de que es la que rodea a la media luna. ¿Cuál será su radio si suponemos que el lado de los cuadrados mide \(a\)?
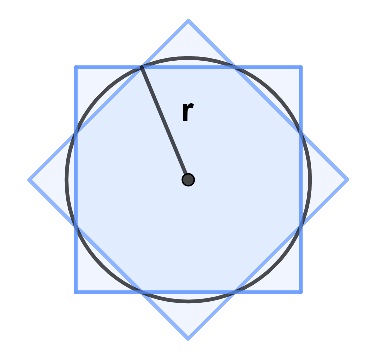
Trabajemos con el triángulo y algunos de los segmentos marcados en la siguiente figura:
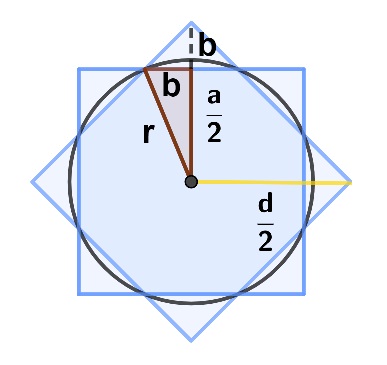
Comencemos calculando la longitud del segmento discontinuo \(b\), que, por simetría, mide lo mismo que el lado más pequeño del triángulo marrón.
\(b=\frac{d}{2}-\frac{a}{2}\), siendo \(d\) la diagonal de los cuadrados.
Por el teorema de Pitágoras:
\[(\frac{d}{2})^2+(\frac{d}{2})^2=a^2\]
\[\frac{d}{2}=\sqrt{\frac{a^2}{2}}=a\frac{\sqrt{2}}{2}\]
Por tanto,
Se puede llegar a este mismo resultado utilizando trigonometría puesto que los puntos de intersección de las aristas de los dos cuadrados forman un octógono regular (inscrito en la circunferencia), que puede ser dividido en ocho triángulos isósceles cuyos ángulos desiguales miden 45o. Una mitad de uno de estos triángulos es el representado en marrón. El valor del ángulo cuyo vértice está en el centro de la circunferencia es 22.5o y, aplicando trigonometría, \(b=\frac{a}{2}\tan 22,5^o\). No obstante, creo que para el común de los mortales es más conocido el Teorema de Pitágoras que las relaciones trigonométricas y, además, para mi gusto, es más bonita la expresión anterior que esta última. Así que continuaré con la primera: \(b=\frac{\sqrt{2}-1}{2}a\).
Si aplicamos de nuevo el Teorema de Pitágoras en el triángulo marrón, hallaremos cuál es valor del radio de la circunferencia:
\[r^2=(\frac{a}{2})^2+(\frac{\sqrt{2}-1}{2}a)^2\]
\[r^2=(\frac{a}{2})^2\cdot[1^2+(\sqrt{2}-1)^2]\]
\[r^2=(\frac{a}{2})^2\cdot(1+2-2\sqrt{2}+1)\]
\[r^2=(\frac{a}{2})^2\cdot(4-2\sqrt{2})\]
\[r=\sqrt{(\frac{a}{2})^2\cdot(4-2\sqrt{2})}\]
\[r=\frac{a}{2}\sqrt{4-2\sqrt{2}}=\frac{\sqrt{4-2\sqrt{2}}}{2}a\]
Con todos los cálculos que hemos hecho, averiguar el área total de la estrella andalusí según el lado de los cuadrados es sencillo, pues podemos calcular el área del octógono central y sumarle las áreas de los ocho triangulitos de alrededor.
El área del octógono se puede calcular usando la fórmula para calcular el área de cualquier polígono regular: \(A=\frac{P·ap}{2}\) (área igual a perímetro por apotema entre dos) o calculando el área de uno de los ochos triángulos isósceles iguales en los que se divide el octógono y multiplicándola por ocho. Pienso que cuantas menos fórmulas tengamos que memorizar, mejor. Así evitamos que se nos olviden. Por tanto, lo vamos a hacer del último modo:
La base de cada uno de esos ocho triángulos es \(2b\). Es decir, \(2b=2\frac{\sqrt{2}-1}{2}a=(\sqrt{2}-1)a\).
La altura de cada triángulo es la mitad del lado del cuadrado, \(\frac{a}{2}\). Por tanto, el área de uno de los ocho triángulos es: \(A_T=\frac{(\sqrt{2}-1)a\frac{a}{2}}{2}=\frac{\sqrt{2}-1}{4}a^2\).
Como el octógono está formado por ocho triángulos iguales, el área del octógono central es \(A_O=8\frac{\sqrt{2}-1}{4}a^2=2(\sqrt{2}-1)a^2\).
En cuanto a los triangulitos pequeños, la base de todos ellos coincide con las de los ocho triángulos en los que se divide el octógono \(2b=(\sqrt{2}-1)a\) y la altura de cada uno de ellos es igual a \(b=\frac{\sqrt{2}-1}{2}a\).
Por tanto, el área de cada triangulito es: \(A’_T=\frac{(\sqrt{2}-1)a\cdot\frac{\sqrt{2}-1}{2}a}{2}=\frac{(\sqrt{2}-1)^2}{4}a^2=\frac{3-2\sqrt{2}}{4}a^2\)
Finalmente, el área de la estrella andalusí es: \[A_E=A_O+8A’_T=2(\sqrt{2}-1)a^2+8\frac{3-2\sqrt{2}}{4}a^2=2a^2(\sqrt{2}-1+3-2\sqrt{2})=2(2-\sqrt{2})a^2\].
En la Resolución de 13 de junio de 2014 no nos dicen qué proporción del área del círculo central está ocupada por la media luna que embute a la cabra, pero usando el método de Montecarlo podemos calcularla.
El método de Montecarlo es un método que permite obtener soluciones a problemas matemáticos o físicos por medio de la repetición de pruebas aleatorias. En la práctica, en lugar de realizar pruebas aleatorias, se realizan cálculos utilizando números aleatorios.
El origen del método de Montecarlo lo encontramos en los trabajos para mejorar la toma de decisiones en condiciones de incertidumbre realizados por John von Newmann y Stanislaw Ulam durante la II Guerra Mundial.
Al parecer la idea se le ocurrió a Ulam mientras estaba enfermo (como a Descartes con los ejes de coordenadas) en 1946. Se dio cuenta de que era más sencillo tener una idea del resultado general del solitario haciendo pruebas con múltiples cartas y contando las proporciones de los resultados, que calcular todas las posibles combinaciones de manera formal. Y pensó que esto mismo se podía aplicar al trabajo sobre difusión de neutrones que estaba desarrollando junto a von Newmann en el Laboratorio Nacional de Los Álamos, puesto que es prácticamente imposible resolver las ecuaciones integrales y diferenciales que describen la dispersión, la absorción y la fisión de las partículas.
Una simulación aplicando el método de Montecarlo crea un modelo de resultados posibles siguiendo una distribución de probabilidad. Cada vez que se repite utiliza un conjunto diferente de números aleatorios y tras realizarlo miles de veces se genera un número enorme de resultados probables. Así, si, por ejemplo, queremos estimar el valor del número π podemos dibujar un círculo radio 1 y un cuadrado que lo circunscriba, de lado 2. La proporción del área del cuadrado ocupada por el círculo es \(\frac{\pi ·1^2}{2^2}=\frac{\pi}{4}\) y esta ha de aproximarse a la proporción de puntos aleatoriamente lanzados que estén sobre el círculo con respecto a todos los que estén sobre el cuadrado. Si lanzamos un millón de puntos \(\frac{\pi}{4}=\frac{a}{1 000 000}\Longrightarrow \pi=\frac{4a}{1 000 000}\), siendo \(a\) el número de puntos aleatorios que ha caído dentro del círculo.
El método de Montecarlo recuerda al experimento de la aguja de Buffon, que es un problema clásico de probabilidad geométrica que planteó por primera vez en 1733 el naturalista francés Georges-Louis Leclerc de Buffon (1707-1788) y que resolvió él mismo en 1777.
Consiste en lanzar una aguja sobre un papel en el que se han dibujado una serie de rectas paralelas todas ellas a la misma distancia.
- Si la distancia entre las rectas es igual a la longitud de la aguja, se puede demostrar que la probabilidad de que la aguja cruce a alguna de las rectas es \(\frac{2}{\pi}\), con lo cual \(\pi\thickapprox \frac{2N}{A}\), siendo \(N\) el número de veces que se ha lanzado la aguja y \(A\) el número de veces que la aguja a cruzado a alguna de las rectas.
- Si la distancia entre las rectas es mayor que la longitud de la aguja se puede demostrar que la probabilidad de que la aguja cruce a las rectas disminuye de manera proporcional a la longitud de la aguja entre la distancia entre las rectas: \(\frac{2L}{D\pi}\) con lo cual, en esta ocasión \(\pi\thickapprox \frac{2NL}{AD}\), siendo \(L\) la longitud de la aguja y \(D\) la distancia entre las rectas.
- Si la distancia entre las rectas es menor que la longitud de la aguja el resultado que se obtiene es más complicado y dejamos a las personas interesadas que busquen información sobre él.
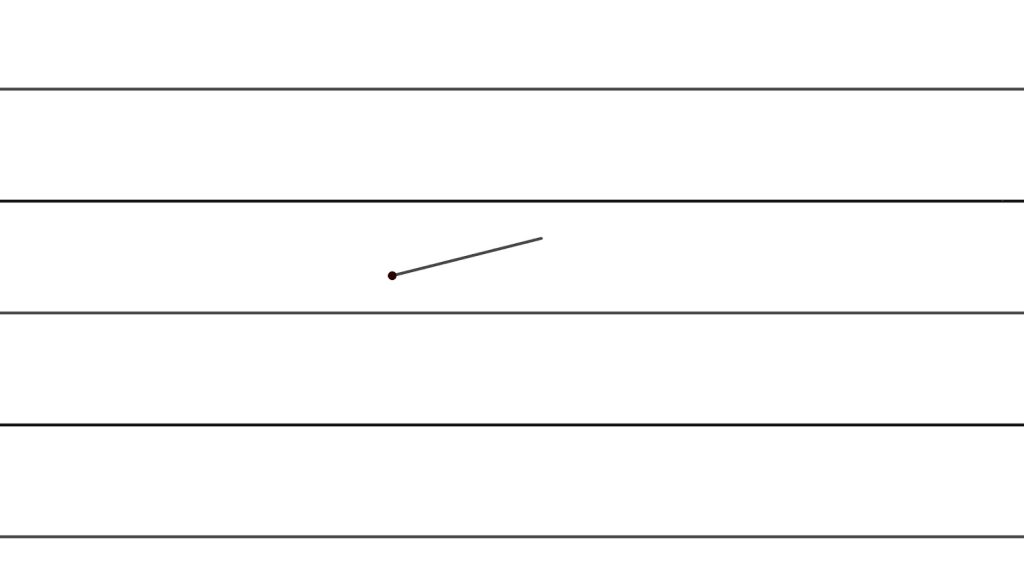
Una generalización de este problema es el problema de la Aguja de Buffon-Laplace, el cual consiste en lanzar la aguja sobre una cuadrícula en lugar de sobre un papel rayado. Recibe este nombre porque Buffon lo resolvió en 1777, pero contenía errores que corrigió Laplace en 1812.
En la actualidad el método de Montecarlo se utiliza para evaluar riesgos y realizar predicciones a largo plazo. Por ejemplo, una persona que sea profesional del marketing si tiene que decidir acerca de aumentar el presupuesto en publicidad para un determinado producto puede utilizar el método de Montecarlo sobre el coste de la publicidad, las retenciones, la previsión del número de unidades vendidas, … El resultado de la aplicación del método le dirá cuál es el impacto de la inversión en publicidad sobre esos factores para así saber si la decisión es rentable o no. Del mismo modo, en los juegos online, los programadores utilizan el método de Montecarlo para simular los resultados de las partidas y así garantizar que el juego es justo, puesto que esto es lo que esperan los jugadores: que el juego sea justo y similar al juego presencial. En el sector de la ingeniería también se utiliza el método de Montecarlo. En este caso el objetivo es garantizar la fiabilidad de los productos que ponen al servicio de las personas y para ello simulan los fallos probables de los mismos en función de las variables existentes.
Podemos encontrar más ejemplos en diferentes sectores, pero no era ese nuestro objetivo sino saber en qué consiste el método de Montecarlo y cómo aplicarlo para averiguar qué proporción del área del círculo de la marca turística de Cabra está ocupada por la media luna. Para ello ayudémonos de GeoGebra que nos va a permitir simular el lanzamiento de puntos de manera aleatoria sobre el círculo. Pincha sobre al imagen, mueve el deslizador y comienza a generar puntos de manera aleatoria.
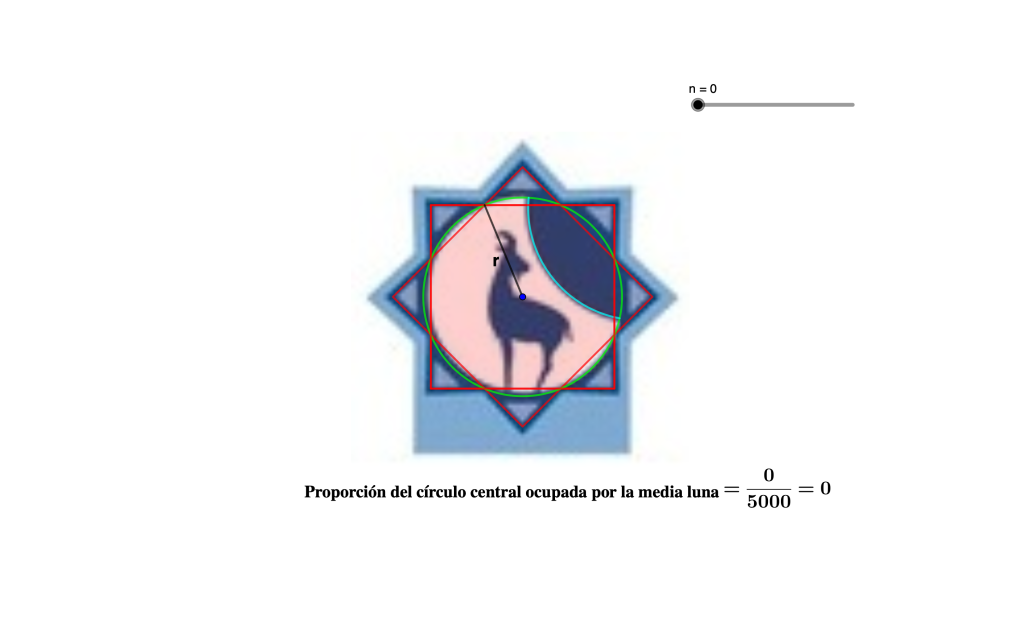
En este caso la aplicación que he hecho genera 5000 puntos sobre el círculo interior. Conforme vamos moviendo el deslizador van cambiando los puntos aleatorios hasta llegar a tener 5000 puntos. Cada vez que repetimos el proceso, generamos 5000 puntos aleatorios distintos, con lo cual si repetimos muchas veces el proceso vemos que la proporción de puntos dentro de la media luna está en torno al 72% (=0,72). Por tanto, el área que ocupa la media luna es aproximadamente \(0,72·\pi r^2=0,72·\pi \frac{4-2\sqrt{2}}{4}a^2=0,72·\pi \frac{2-\sqrt{2}}{2}a^2\), siendo \(a\) la longitud del lado de los cuadrados.
Del mismo modo podríamos calcular el área que ocupa la cabra dentro de la media luna, pero definir las restricciones de esta figura es mucho más complicado. Si alguien se anima, que me escriba y nos ponemos a ello. 😉
¡Buen otoño y buenas matemáticas!