Son muchas las banderas que existen y es evidente que son una fuente de actividades matemáticas. Basta con pensar en combinatoria y comenzamos a hacernos una idea. Pero, además de esta idea que sale de manera natural, hay banderas que por las formas que aparecen en ellas dan más juego aún; y eso le ocurre a la bandera de Cabra (Córdoba).
En el Boletín Oficial de la Junta de Andalucía número 122 del 26 de junio de 2014 aparece publicada la Resolución de 13 de junio de 2014, de la Dirección General de Administración Local, por la que se admite la inscripción en el Registro Andaluz de Entidades Locales del escudo, la bandera, el logotipo y la marca turística del municipio de Cabra (Córdoba). En ella se describen el escudo, la bandera, el logotipo y la marca turística de Cabra. Centrémonos en la bandera y ya dedicaremos otra entrada a la marca turística.
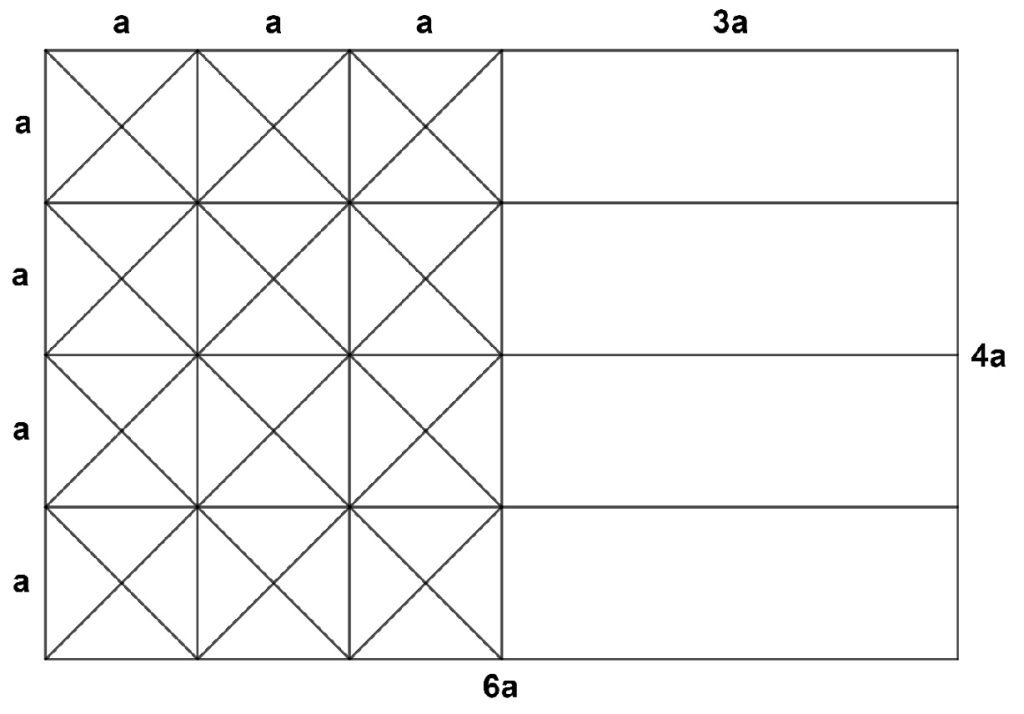
La bandera tiene forma rectangular y está dividida verticalmente en dos partes iguales:
- La primera, la que pega al mástil, contiene cuatro franjas de tres cuadrados cada una. Cada uno de estos cuadrados está formado por la unión de cuatro triángulos isósceles de colores rojo, blanco, amarillo y verde, comenzando la primera y tercera de las franjas por un triángulo rojo y la segunda y la cuarta por un triángulo amarillo. Los triángulos rojos y amarillos siempre se sitúan longitudinalmente opuestos a los triángulos de colores verde y blanco.
- La segunda mitad está compuesta por cuatro franjas iguales que, de arriba a abajo, son de colores rojo, amarillo, blanco y verde. Cada una de estas franjas coincide longitudinalmente con cada una de las series de cuadrados de la primera mitad. Centrado en la segunda mitad, y ocupando las franjas amarillas y blanca, se sitúa el escudo de Cabra.

La primera pregunta que se me ocurre es: ¿qué proporción existe entre el largo y el ancho de la bandera?
Supongamos que cada lado desigual de los triángulos isósceles mide \(a\), con lo cual la anchura de cada franja horizontal mide \(a\) y, por tanto, el ancho de la bandera es \(4a\). Del mismo modo, la mitad de la bandera mide \(3a\), puesto que está compuesta por tres columnas de cuatro cuadrados de lado \(a\). Así, el largo de la bandera es \(6a\) y la proporción entre el largo y el ancho es \(\frac{6a}{4a}=\frac{3}{2}\), es decir 3:2.
¿Casualidad? Puede que sí o tal vez no, porque según el Real Decreto 1511/1977, de 21 de enero, por el que se aprueba el Reglamento de Banderas y Estandartes, Guiones, Insignias y Distintivos, la proporción entre el largo y el ancho de la bandera de España es la misma y, además, según el punto 2 del artículo sexto de la Ley 39/1981, de 28 de octubre, por la que se regula el uso de la bandera de España y el de otras banderas y enseñas, si junto a la bandera de España ondean otras, estas no podrán tener un tamaño mayor al de la nacional. Si la bandera de España y la bandera de Cabra tienen la misma proporción, igual es más fácil evitar problemas con el tamaño, porque ¿a qué se refiere con el tamaño? ¿A la superficie? ¿Al ancho? ¿Al largo? ¿A las dos cosas?

Si la bandera de Cabra fuese cuadrada, como la de la Virgen de la Sierra, y tuviera que ponerse al lado de la de España; y si suponemos que con lo de no superar el tamaño de la bandera de España se está refiriendo a la superficie, el lado de la bandera cuadrada tendría que ser \(\sqrt{\frac{3}{2}}a\) puesto que el área de la bandera de España es \(\frac{3}{2}a\cdot a=\frac{3}{2}a^2\) y un cuadrado con esa superficie tendrá de lado \(\sqrt{\frac{3}{2}a^2}=\sqrt{\frac{3}{2}}a\).
Pero volvamos a la bandera de Cabra, donde encontramos otras cuestiones que pueden ser interesantes. ¿Cuánto miden los lados iguales de los triángulos isósceles? Es evidente que son triángulos isósceles y rectángulos, puesto que las diagonales de cualquier cuadrado se cortan perpendicularmente y cuatro de estos triángulos forman un cuadrado. Así que el Teorema de Pitágoras va a ser nuestro gran aliado:
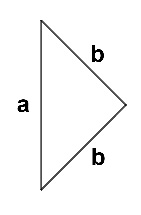 | \[a^2=b^2+c^2\] \[a^2=2b^2\] \[\frac{a^2}{2}=b^2\] \[b=\sqrt{\frac{a^2}{2}}\] \[b=a\sqrt{\frac{1}{2}}\] \[b=a\frac{\sqrt{2}}{2}\] |
Por tanto, los lados iguales de los triángulos miden \(\frac{\sqrt{2}}{2}a\), siendo \(a\) la longitud del lado desigual de los triángulos, o lo que es lo mismo un cuarto de la anchura de la bandera. Con lo cual los lados iguales de los triángulos miden \(\frac{\sqrt{2}}{8}\) de la anchura de la bandera.
El número de triángulos de cada color es el mismo: hay 12 triángulos rojos, 12 amarillos, 12 verdes y 12 blancos; y el tamaño de las franjas es el mismo en todos los casos. Por tanto, un cuarto de bandera es rojo, un cuarto es amarillo, un cuarto es verde y un cuarto es blanco, pero ¿qué proporción existe entre el espacio que ocupan los triángulos rojos de la primera franja y la franja roja?
La franja roja tiene por área \(3a^2\), veamos qué superficie ocupan los triángulos rojos de esa franja.
Esta pregunta se puede responder lanzándonos a calcular el área de cada triángulo puesto que ya conocemos cuánto mide la base y la altura, \(\frac{\sqrt{2}}{2}a\):
cosa que es evidente puesto que los cuatro triángulos, que son iguales, forman un cuadrado de lado \(a\), con lo cual el área de cada uno de esos triángulos es un cuarto del área del cuadrado.
Pero también podemos pararnos a pensar un poco. Si en la primera franja hay tres triángulos rojos, estos ocupan una superficie equivalente a \(\frac{3}{4}\) de un cuadrado de lado \(a\). Por tanto, el área que ocupan los tres triángulos rojos es \(\frac{3}{4}a^2\). Tres veces el área de un triángulo.
Así pues, la proporción entre los triángulos rojos de la primera franja y la franja roja es:
\[\frac{\frac{3}{4}a^2}{3a^2}=\frac{1}{4}\]
Cosa que también podríamos haber deducido pensando que la franja roja ocupa lo mismo que los tres cuadrados de la primera franja y que estas están compuestas por un cuarto de triángulos de cada color.
Como vemos las matemáticas son unas grandes aliadas, pero, en ocasiones, fijándonos un poco, podemos extraer conclusiones numéricas sin necesidad de hacer cálculos. Dejamos como muestra la siguiente pregunta para que intentéis resolverla sin hacer cálculos: ¿qué proporción existe entre todos los triángulos de cada color y su correspondiente franja?
¡Buen verano y buenas matemáticas! ¡Y buenas fiestas en honor a la Virgen de la Sierra!
Egabrenses, cuando os metáis debajo de la bandera, acordaos de que también estáis bajo muchas matemáticas. 😉